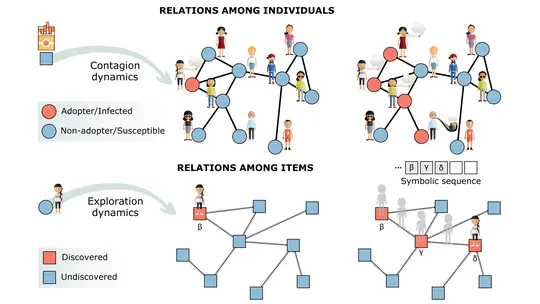
Welcome! Our group uses an interdisciplinary approach that combines physics, mathematics, data, and network science to provide insights into the complexity of social systems and behaviors, particularly in the areas of behavioral contagion, discovery processes, and group dynamics.
We are part of the Network Science Institute at Northeastern University London.

Latest Blog Posts
How do groups form and evolve? How do individuals navigate these group structures?
Higher-order naming game: combining group dynamics ans social influence
New perspective article on the dual nature of adoption processes
Featured Publications
(2025).
The dynamics of higher-order novelties.
Nature Communications.
(2024).
The temporal dynamics of group interactions in higher-order social networks.
Nature Communications.
(2023).
Hyper-cores promote localization and efficient seeding in higher-order processes.
Nature Communications.
(2022).
Non-selective distribution of infectious disease prevention may outperform risk-based targeting.
Nature Communications.
(2021).
The physics of higher-order interactions in complex systems.
Nature Physics.
(2020).
Interactive discovery processes on complex networks.
Physical Review Letters.