How can minorities of regular individuals overturn social conventions?

Higher-order naming game: combining group dynamics ans social influence

Last updated on May 8, 2024 6 min read
Ph by Markus Spiske

Our study “Group interactions modulate critical mass dynamics in social convention” is out on Communications Physics!

How can minorities of regular individuals overturn social conventions? The theory of critical mass argues that apparently stable social conventions can be overturned by a minority of committed individuals if such minority reaches a critical size. Several studies have focused on identifying this critical size.

Ph by Benedikt Geyer

Qualitative studies of gender conventions in corporate leadership roles have hypothesised that a critical mass of 30% of the population is necessary in order for the tipping point to be reached. Related observational work on gender research has proposed a higher critical mass size approaching 40% of the population.

Quantitative support to the tipping points dynamics has come from the naming game model for social convention, where a critical mass of 10% was shown to be able to induce norm change. Subsequent generalisations showed how the threshold can vary between 10% and 40% of the population. Finally, controlled experiments of social coordination have brought empirical evidence for tipping points in the dynamics of social conventions, finding a critical threshold of 25% of the population, as theoretically predicted by a best response naming game model.

Ph by Callum Shaw

All theoretical models and empirical studies existing so far have considered minority groups of fully committed individuals, i.e., individuals who will not adopt majoritarian conventions under any circumstances. In this light, even 10% of the population, the smallest threshold obtained thus far, can hardly be considered a “small” group. Numerous observations suggest that even groups counting just tens of committed individuals, and not significant fractions of the population, may trigger abrupt social and normative change. Social movements offer several examples in this sense. So… where does the critical mass itself come from?

In this new work, together with G. Petri, A. Baronchelli and A. Barrat, we give a mechanistic explanation of how such small minorities can emerge. In particular, we show that the critical mass required to induce norm change is dramatically reduced when non-committed members of the population are less susceptible to social influence than previously assumed.

Dynamics of the model. Agents are represented by the nodes of a social structure composed by interacting groups of different sizes. The vocabulary of the agents–for simplicity containing at most only two names (or conventions) ${A, B}$–is reflected in the colours of the nodes as shown in the legend. At each interaction a group is chosen at random (highlighted in yellow in the figure) together with a speaker (node 1), while the remaining nodes act as hearers. (A) The speaker chooses a name at random from its vocabulary (here, $A$), and communicates it to the rest of the group. Since $A$ is present in the vocabularies of all the hearers (nodes 2 and 3 support $A$, while node 4 knows both names), the group can reach an agreement. (B) With probability $\beta$ the group agrees on the chosen name, and all nodes involved immediately update their vocabulary to $A$, erasing $B$. With probability $1-\beta$ instead the agreement does not happen. (C) In this case, the speaker selects $A$, but node 3 does not possess $A$ in its vocabulary. (D) Thus, there cannot be agreement in the group. Nevertheless, all hearers update their vocabularies by adding the heard name, i.e., node 3 switches from $A$ to $A, B$.

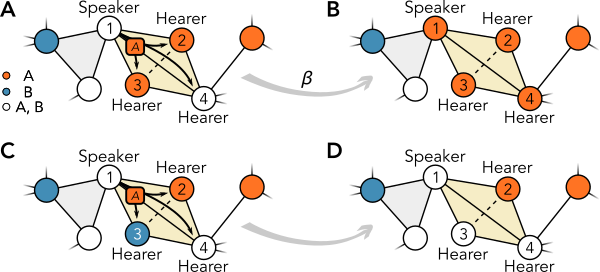
We adopt the Naming Game framework, already used to determine the range of 10% to 40% critical mass thresholds, and admit the possibility that individuals may be reluctant to let go of alternative conventions even when they successfully manage to coordinate with one another on a specific norm. We control this through a global communication efficiency parameter $\beta \in [0,1]$. This generalises the standard naming game model where a successful coordination is followed by a certain and exclusive adoption of the norm that allowed the coordination.

Illustrative example of a simulation on an empirical social structure (contacts in a French high-school) where a minority of one single committed individual supporting $A$–consisting of 0.3% of the population of 327 individuals–overturns the stable social norms and reaches global consensus (under imperfect communication). (F) Temporal evolution of the fraction $n_x(t)$ of nodes supporting name $x$. Different solid lines correspond to different names, $x={A+A_c, B, (A, B)}$. Dashed lines are reported as a benchmark, representing the case with perfect communication.

We inform the model with real-world data concerning the structure of the social networks and of the microscopic interactions, considering both pairwise and group meetings. This implies using a higher-order representation beyond pairwise interactions, as the one offered by hypergraphs.

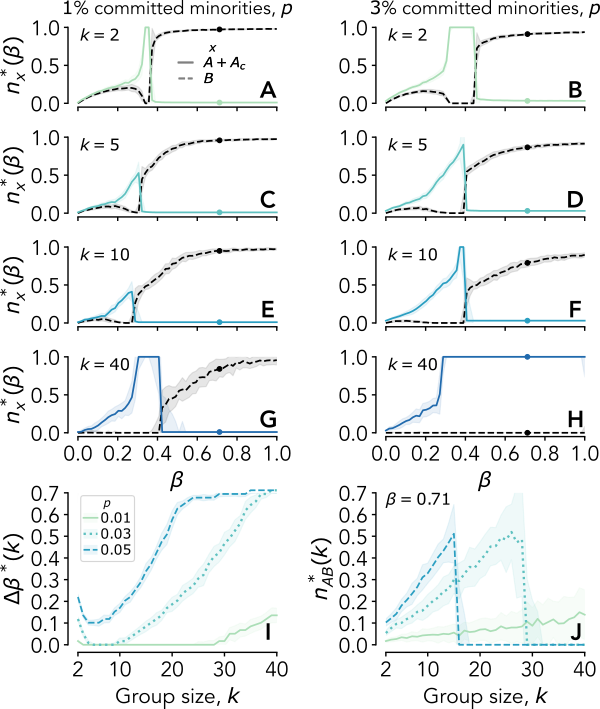
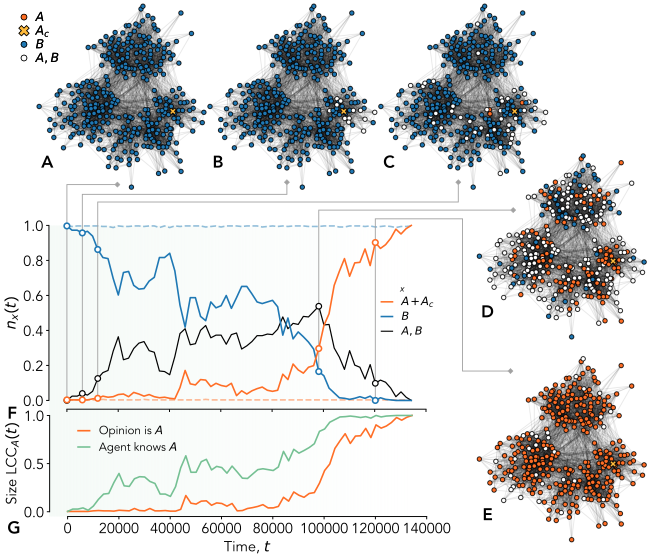
Higher-order (group) effects in naming games for different values of $\beta$. We consider $(k-1)-$uniform hypergraphs, i.e. regular structures in which each interaction involves exactly $k$ agents. (A-H) Left and right panels correspond to simulations initiated with a different size of committed minority supporting opinion $A$, namely $p=0.01$ and $p=0.03$. In the initial state, all the other agents hold norm $B$. The range $\Delta\beta^$ of $\beta$ values for which $n^_A=1$ (i.e., the committed minority manages to convert the whole population), is plotted in (I) as a function of the group size $k$ and for different values of $p$ (see legend).

We show that results hold in a significant region of the parameters and on all the considered real and artificial social structures. In addition, we clarify the role of group interactions showing a non-trivial dependency of the long term dynamical output with the group-size (non-monotonicity is observed). We also provide an analytical mean-field description of the model and confirm its accuracy against Monte Carlo simulations.

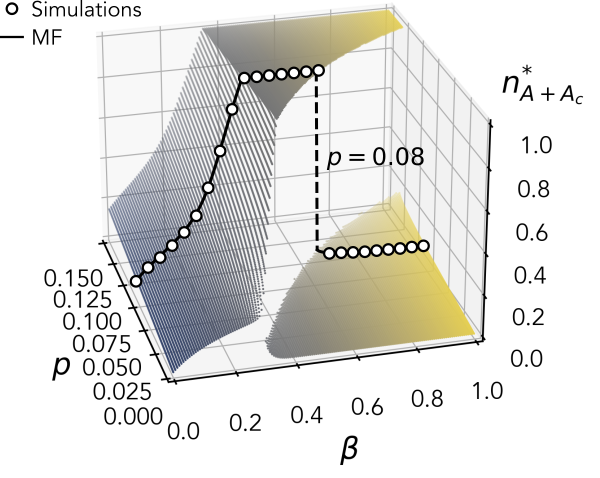
Mean field phase diagram of the NG with committed minorities on 2-uniform hypergraphs. An example curve with $p=0.08$ is shown with a solid black line. The associated results of stochastic simulations (circles) for homogeneous systems of $1000$ agents are shown for comparison.

Our findings reconcile the numerous observational accounts of rapid change in social conventions triggered by committed minorities with the apparent difficulty of establishing such large minorities.

In this scenario, clarifying the microscopic mechanisms driving this process is key to gain a better understanding of our society and to design possible interventions aimed at contrasting undesired effects (see recent studies about social media infiltrations by the Chinese government).

On the other hand, understanding how policy can create tipping points where none exist and how it can push the system past the tipping point are fundamental questions whose answer might change the way in which we address major societal challenges, such as accelerating the post-carbon transition or contrasting vaccine-hesitancy.

Ph by Belinda Fewings
Higher-order Naming game Social convention Tipping points Critical mass Hypergraphs Social dynamics
Iacopo Iacopini
Iacopo Iacopini
Associate Professor

My research interests include complex networks, social systems, and cities.

Next
Previous

Related