The dynamics of higher-order novelties

Abstract

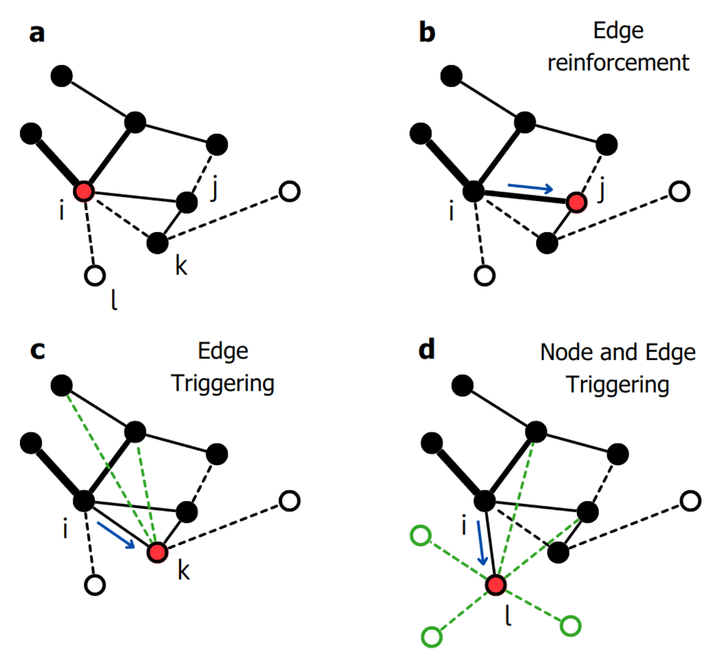
The Heaps’ law, which characterises the growth of novelties, has triggered new mathematical descriptions, based on urn models or on random walks, of the way we explore the world. However, an often overlooked aspect is that novelties can also arise as new combinations of existing elements. Here we propose to study novelties as n>=1 consecutive elements appearing for the first time in a sequence, and we introduce the nth-order Heaps’ exponents to measure the pace of discovery of novelties of any order. Through extensive analyses of real-world sequences, we find that processes displaying the same pace of discovery of single items can instead differ at higher orders. We then propose to model the exploration dynamics as an edge-reinforced random walk with triggering on a network of relations between items which evolves over time. The model reproduces the observed properties of higher-order novelties, and reveals how the space of possibilities expands over time along with the exploration process.