Abstract
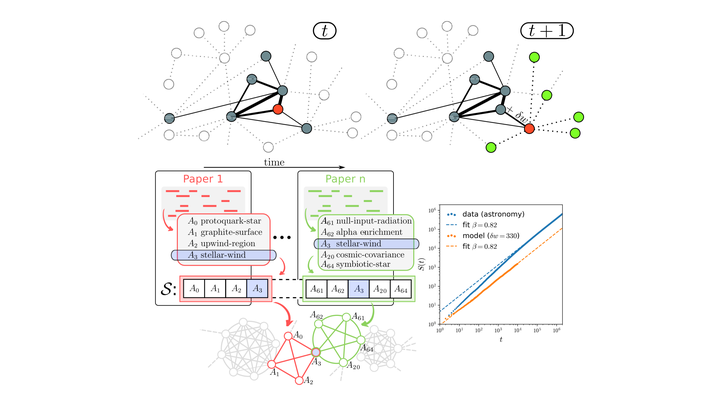
We introduce a model for the emergence of innovations, in which cognitive processes are described as random walks on the network of links among ideas or concepts, and an innovation corresponds to the first visit of a node. The transition matrix of the random walk depends on the network weights, while in turn the weight of an edge is reinforced by the passage of a walker. The presence of the network naturally accounts for the mechanism of the adjacent possible, and the model reproduces both the rate at which novelties emerge and the correlations among them observed empirically. We show this by using synthetic networks and by studying real data sets on the growth of knowledge in different scientific disciplines. Edge-reinforced random walks on complex topologies offer a new modeling framework for the dynamics of correlated novelties and another example of co-evolution of processes and networks.