Simplicial contagion in temporal higher-order networks
Abstract
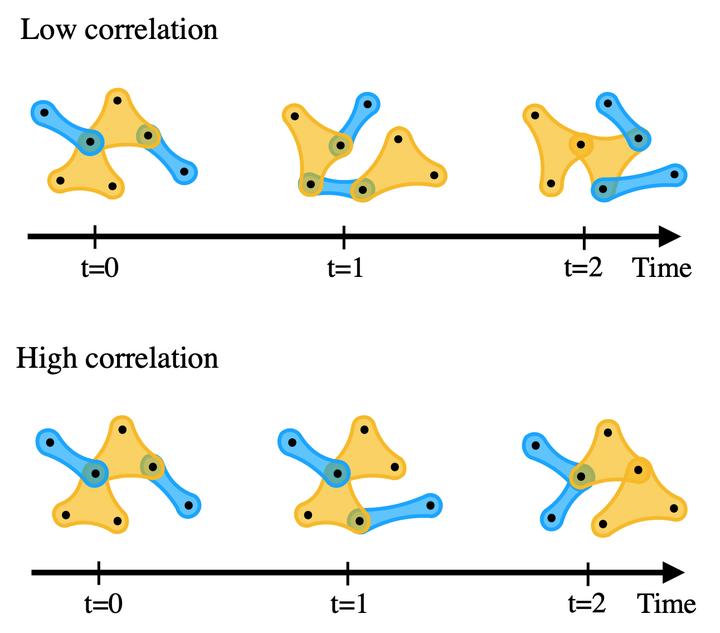
Complex networks represent the natural backbone to study epidemic processes in populations of interacting individuals. Such a modeling framework, however, is naturally limited to pairwise interactions, making it less suitable to properly describe social contagion, where individuals acquire new norms or ideas after simultaneous exposure to multiple sources of infections. Simplicial contagion has been proposed as an alternative framework where simplices are used to encode group interactions of any order. The presence of these higher-order interactions leads to explosive epidemic transitions and bistability. In particular, critical mass effects can emerge even for infectivity values below the standard pairwise epidemic threshold, where the size of the initial seed of infectious nodes determines whether the system would eventually fall in the endemic or the healthy state. Here we extend simplicial contagion to time-varying networks, where pairwise and higher-order simplices can be created or destroyed over time. By following a microscopic Markov chain approach, we find that the same seed of infectious nodes might or might not lead to an endemic stationary state, depending on the temporal properties of the underlying network structure, and show that persistent temporal interactions anticipate the onset of the endemic state in finite-size systems. We characterize this behavior on higher-order networks with a prescribed temporal correlation between consecutive interactions and on heterogeneous simplicial complexes, showing that temporality again limits the effect of higher-order spreading, but in a less pronounced way than for homogeneous structures. Our work suggests the importance of incorporating temporality, a realistic feature of many real-world systems, into the investigation of dynamical processes beyond pairwise interactions.