Abstract
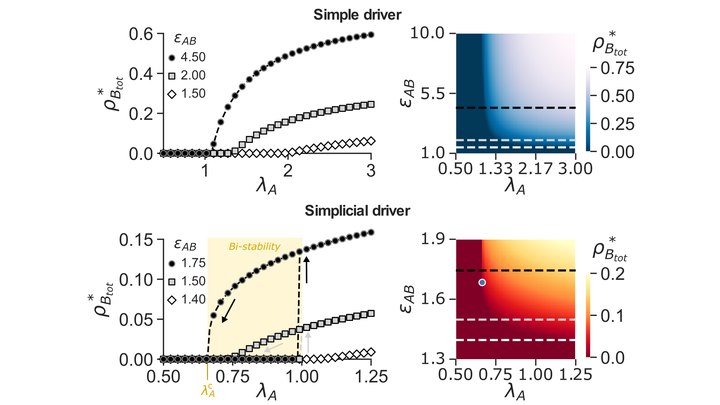
Single contagion processes are known to display a continuous transition from an epidemic-free state to an epidemic one, for contagion rates above a critical threshold. This transition can become discontinuous when two simple contagion processes are coupled in a bidirectional symmetric way. However, in many cases, the coupling is not symmetric and the nature of the processes can differ. For example, risky social behaviors—such as not wearing masks or engaging in large gatherings—can affect the spread of a disease, and their adoption dynamics via social reinforcement mechanisms are better described by complex contagion models rather than by simple contagions, more appropriate for disease spreading. Here, we consider a simplicial contagion (describing the adoption of a behavior) that unidirectionally drives a simple contagion (describing a disease propagation). We show, both analytically and numerically, that, above a critical driving strength, such a driven simple contagion can exhibit both discontinuous transitions and bistability, absent otherwise. Our results provide a route for a simple contagion process to display the phenomenology of a higher-order contagion, through a driving mechanism that may be hidden or unobservable in practical instances.