Non-Gaussian power grid frequency fluctuations characterized by Lévy-stable laws and superstatistics
Benjamin Schäfer, Christian Beck, Kazuyuki Aihara, Dirk Witthaut & Marc Timme, Nature Energy (2018).
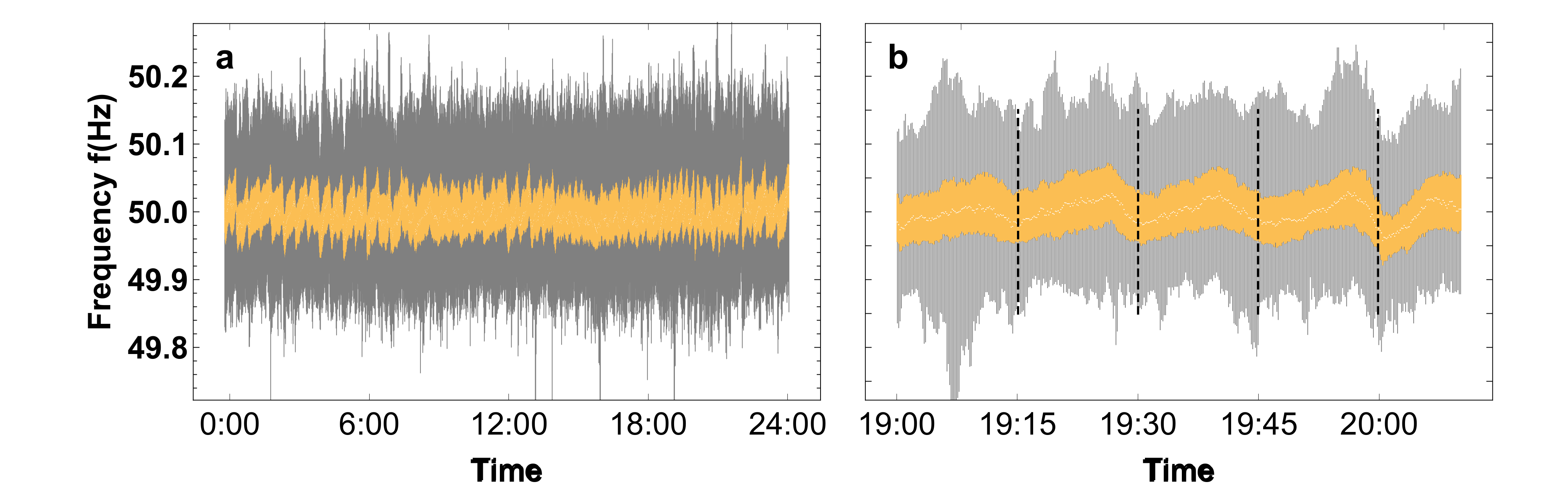
The effect of energy trading is strong and comparable in size to the effect of renewables on the frequency fluctuations of a power grid, according to our new study published with collaborators from Goettingen, Juelich and Tokyo in Nature Energy (link).
We also found that splitting a large grid into small microgrids - as a way of integrating additional renewable power generation or creating smaller, mostly independent grids - will lead to larger frequency deviations which can potentially damage sensitive electronic devices.
Abstract
Multiple types of fluctuations impact the collective dynamics of power grids and thus challenge their robust operation. Fluctuations result from processes as different as dynamically changing demands, energy trading and an increasing share of renewable power feed-in. Here we analyse principles underlying the dynamics and statistics of power grid frequency fluctuations. Considering frequency time series for a range of power grids, including grids in North America, Japan and Europe, we find a strong deviation from Gaussianity best described as Lévy-stable and q-Gaussian distributions. We present a coarse framework to analytically characterize the impact of arbitrary noise distributions, as well as a superstatistical approach that systematically interprets heavy tails and skewed distributions. We identify energy trading as a substantial contribution to today’s frequency fluctuations and effective damping of the grid as a controlling factor enabling reduction of fluctuation risks, with enhanced effects for small power grids.
Press
Network dynamics of innovation processes
Iacopo Iacopini, Staša Milojević & Vito Latora, Physical Review Letters (2018).
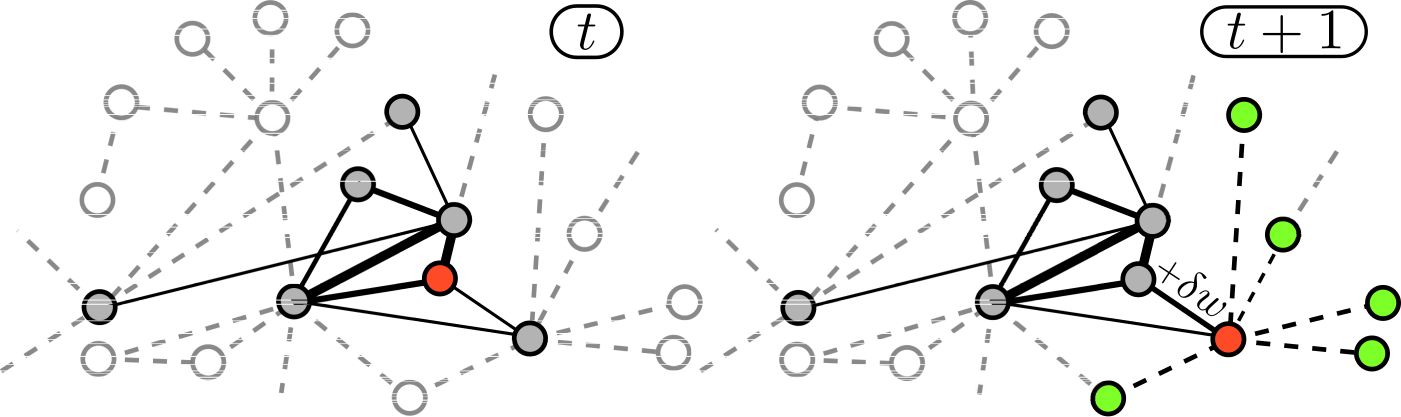
The emergence of innovation can be modelled by using edge-reinfoced random walks over a complex network of concepts and ideas, according to our new study published with our collaborator Staša Milojević from Indiana University in Physical Review Letters (link).
Abstract
Creativity and innovation are the underlying forces driving the growth of our society and economy. The dynamics of innovation has been modeled in different contexts as an evolutionary process or by using the Polya urn framework. We introduce a model for the emergence of innovations, in which cognitive processes are described as random walks (RW) on the network of links among ideas or concepts, and an innovation corresponds to the first visit of a node. The network is co-evolving with the dynamical process taking place over it. In particular, i) biased random walkers move over a network with assigned topology, whose edge weights represent the strength of concept associations, and the transition matrix of the RW depends on the network weights (see Fig); ii) the network evolves in time through a reinforcement mechanism, in which the weight of an edge is increased by a quantity δw every time the edge is traversed by a walker. The presence of the network naturally accounts for the mechanism of the “adjacent possible”, and the model reproduces both the rate at which novelties emerge (Heaps’ law) and the correlations among them observed empirically. We show this by testing our model on synthetic small-world networks and on a real case, in which we consider the growth of knowledge in different scientific disciplines as a discovery process on an underlying network of relations among concepts that can be directly accessed and used from the datasets of 20 years of scientific articles. Edge-reinforced random walks on complex topologies offer a new modeling framework for the dynamics of correlated novelties and another example of co-evolution of processes and networks.
Press
Dynamically induced cascading failures in power grids
Benjamin Schäfer, Dirk Witthaut, Marc Timme & Vito Latora, Nature Communications (2018) - link
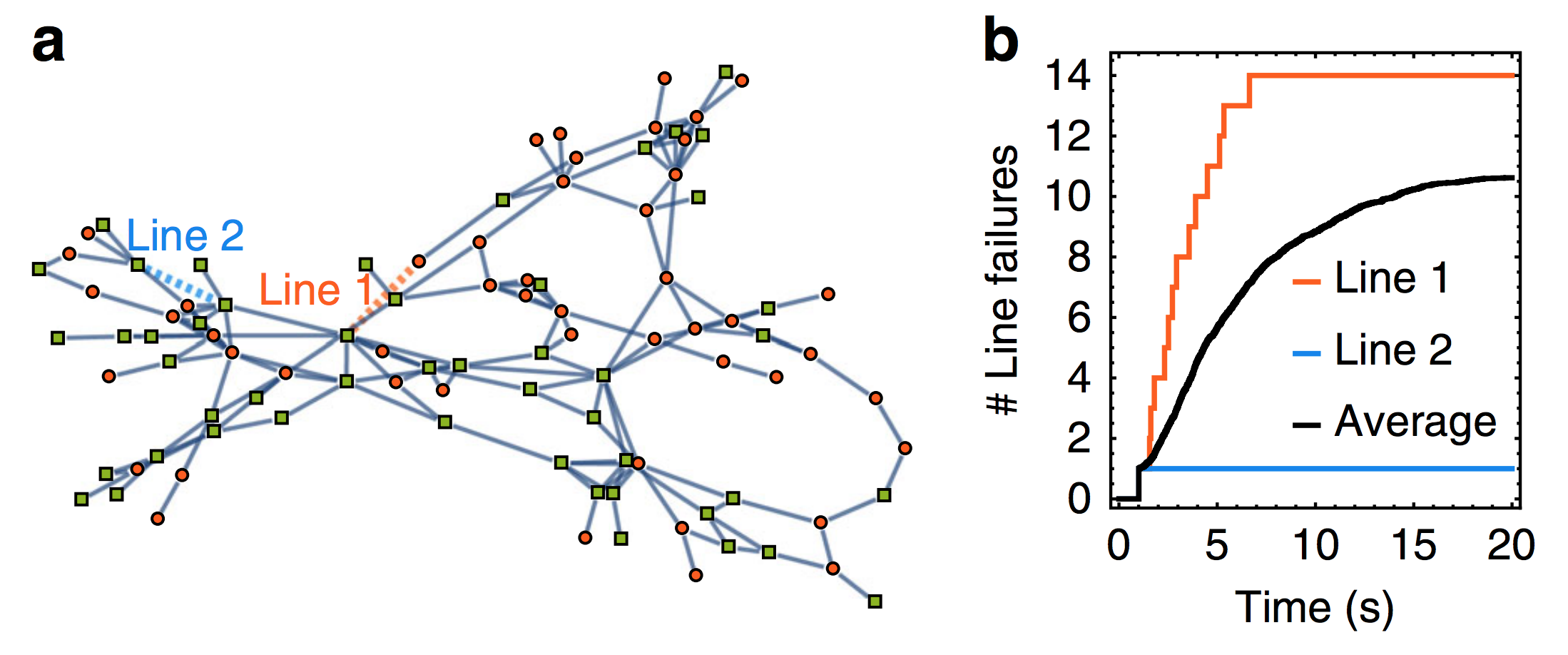
Abstract
Reliable functioning of infrastructure networks is essential for our modern society. Cascading failures are the cause of most large-scale network outages. Although cascading failures often exhibit dynamical transients, the modeling of cascades has so far mainly focused on the analysis of sequences of steady states. In this article, we focus on electrical transmission networks and introduce a framework that takes into account both the event-based nature of cascades and the essentials of the network dynamics. We find that transients of the order of seconds in the flows of a power grid play a crucial role in the emergence of collective behaviors. We finally propose a forecasting method to identify critical lines and components in advance or during operation. Overall, our work highlights the relevance of dynamically induced failures on the synchronization dynamics of national power grids of different European countries and provides methods to predict and model cascading failures.
Benchmarking the performance of controllers for power grid transient stability
Randall Martyr, Benjamin Schaefer, Christian Beck, Vito Latora, Sustainable Energy, Grids and Networks (2019) - link
Abstract
As the energy transition transforms power grids across the globe, it poses several challenges regarding grid design and control. In particular, high levels of intermittent renewable generation complicate the task of continuously balancing power supply and demand, requiring sufficient control actions. Although there exist several proposals to control the grid, most of them have not demonstrated to be cost efficient in terms of optimal control theory. Here, we mathematically formulate an optimal centralized (therefore non-local) control problem for stable operation of power grids and determine the minimal amount of active power necessary to guarantee a stable service within the operational constraints, minimizing a suitable cost function at the same time. This optimal control can be used to benchmark control proposals and we demonstrate this benchmarking process by investigating the performance of three distributed controllers, two of which are fully decentralized, that have been recently studied in the physics and power systems engineering literature. Our results show that cost efficient controllers distribute the controlled response amongst all nodes in the power grid. Additionally, superior performance can be achieved by incorporating sufficient information about the disturbance causing the instability. Overall, our results can help design and benchmark secure and cost-efficient controllers.
Simplicial models of social contagion
Iacopo Iacopini, Giovanni Petri, Alain Barrat & Vito Latora, Nature Communications (2019).
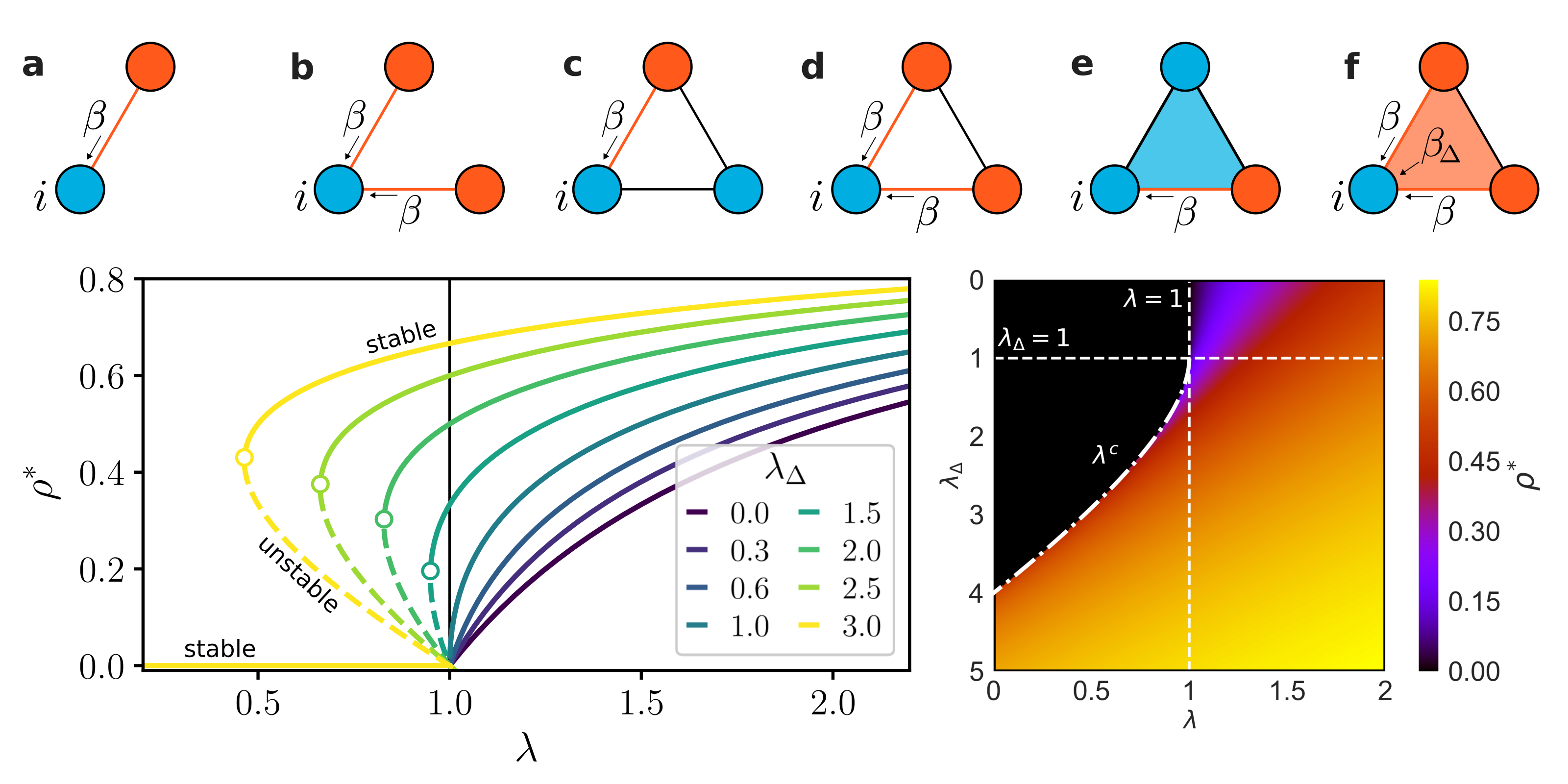
This work introduces the Simplicial Contagion Model (SCM), a novel higher-order modelling framework of social contagions. In the SCM, the structure of a social system is represented as a simplicial complex, and different channels of infections, with different transmission rates, are considered depending on the fact that a contagion can occur on a link (two-body interaction) or is due to a group interaction.
This new study has been published in Nature Communications (link) with collaborators from Turin and Marseille.
Abstract
Complex networks have been successfully used to describe the spread of diseases in populations of interacting individuals. Conversely, pairwise interactions are often not enough to characterize social contagion processes such as opinion formation or the adoption of novelties, where complex mechanisms of influence and reinforcement are at work. Here we introduce a higher-order model of social contagion in which a social system is represented by a simplicial complex and contagion can occur through interactions in groups of different sizes. Numerical simulations of the model on both empirical and synthetic simplicial complexes highlight the emergence of novel phenomena such as a discontinuous transition induced by higher-order interactions. We show analytically that the transition is discontinuous and that a bistable region appears where healthy and endemic states co-exist. Our results help explain why critical masses are required to initiate social changes and contribute to the understanding of higher-order interactions in complex systems.
Multi-layer modelling of adoption dynamics in energy demand management
Iacopo Iacopini, Benjamin Schäfer, Elsa Arcaute, Christian Beck & Vito Latora (2019) - link preprint
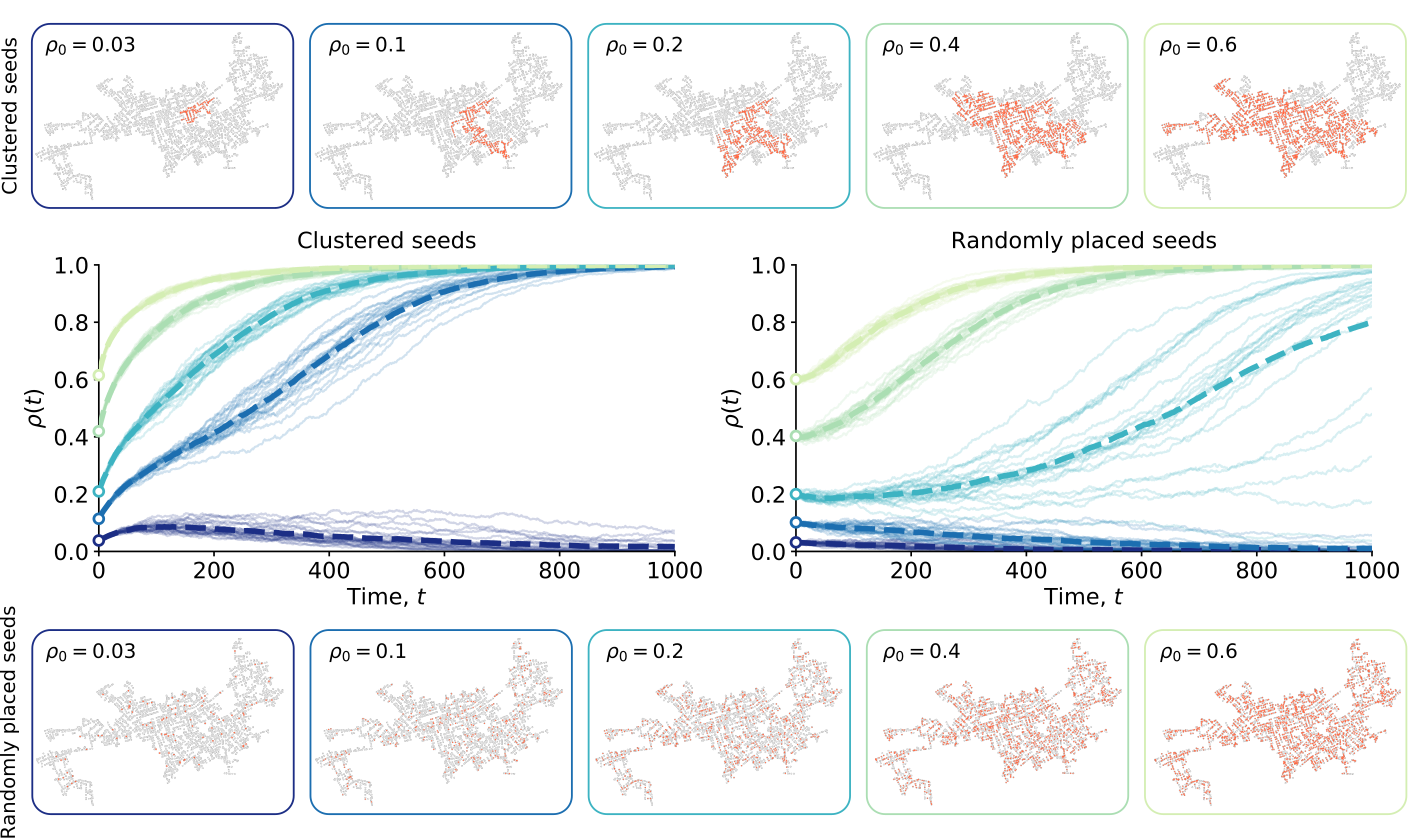
Abstract
Due to the emerging of new technologies, the whole electricity system is undergoing transformations on a scale and pace never observed before. In particular, the decentralisation of energy resources and the smart grid have changed the rules of the game and have forced utility services to rethink their relationships with customers. The so-called demand response (DR) seeks to adjust the demand for power instead of adjusting the supply. However, DR business models rely on customer participation and might only be effective if large numbers of customers in close geographic vicinity, e.g. connected to the same transformer, opt in. Here, we introduce a model for the dynamics of service adoption, in which the behaviour of a customer is influenced by its social contacts, in addition of also depending on the specific spatial configuration of other customers in close proximity within the power grid service area. In particular, we use a multiplex network with two layers coupled together, the social layer among customers and the power-grid layer connecting the households. While the adoption process, modelled as an epidemic spreading, runs on the social layer, the node- and timedependent recovery rate of the nodes depends on the states of their neighbours on the power-grid layer, so that the dynamics tends to preserve clusters of infected individuals by making an infected node surrounded by nodes in the same state less keen to recover. Numerical simulations of the model on synthetic and real-world networks show that strong local influence of the costumers actions leads to a discontinuous transition where either no or all nodes in the network are infected, depending on the infection rate and the social pressure to adopt. We find that clusters of local early adopters act as points of high local pressure, helping maintaining adopters, and facilitating an eventual adoption of all nodes. This suggests direct marketing strategies on how to efficiently establish and maintain new technologies such as DR schemes.